[index Math] Pour discuter de mathématique...

[freeshost]

Bien calculé ! astro !

[freeshost]

C'est l'histoire d'un autre manchot :

Il parcourt d'abord une distance AB de 600 mètres en 15 minutes.
Il parcourt ensuite une distance BC de 1.9 km en 20 minutes.
Il parcourt alors une distance CD de 3.5 km en 28 minutes.
Il parcourt enfin une distance DE de 2.5 km en 30 minutes.

Calculer la vitesse moyenne de marche de ce manchot sur AB, BC, CD et DE.

Calculer la vitesse moyenne de marche de ce manchot sur AE :

- à partir de la distance totale et de la durée totale de marche,
- à l'aide de la moyenne harmonique.

[Tugdual]

-> Un réseau mathématique dans le cerveau ...

[Alone3545]

Sur la vidéo de taupe 10 sur les les vrais infos qui semblent fausse, il est dit que des mathématicien on vu que 1+2+3+4+5+6+... (Infini) = -1/12 pourquoi? Apparemment il n'y aurait pas des canular dans la vidéo. Ets çe vraiment vrai que des mathématiciens ont découvert cela?

[astro]

micmaths l'explique très bien :

https://www.youtube.com/watch?v=xqTWRtNDO3U

Les physiciens s'en servent même dans des expériences "physiques" (dans le sens expériences réelles pas expériences de pensée).

[Ixy]

En vrai il y a des règles sur les séries qui t interdisent d'écrire ce genre de choses.

[astro]

En vrai il y a des règles sur les séries qui t interdisent d'écrire ce genre de choses.

Je dirais "en maths" plutôt qu'en vrai (pourtant j'ai aussi plutôt tendance à considérer les maths comme la vérité en général).
Même sans avoir trouvé comment/pourquoi/une vraie démonstration mathématique, si c'est utilisé avec des résultats probant c'est bien qu'il y a "quelque chose" à creuser sur cette piste du -(1/12).
Il faudrait que je retrouve, je me demande si c'est pas dans des expériences sur l'effet Casimir que ça a une application.

edit : le blog science étonnante en parle, et de manière plus détaillée https://sciencetonnante.wordpress.com/2 ... 34567-112/

[freeshost]

Une brève lecture.

[Alone3545]

Je pense que le résultat -1/12 est en faite un sophisme comme celui-ci en plus élaboré:

Plus il y a de fromage, plus il y a de trou
Plus il y a de trou, moins il y a de fromage

(Donc on en déduit plus il y a de fromage, moins il y a de fromage)

C'est presque exactement pareil pour cette fameuse suite égale à -1/12

[astro]

Pas vraiment non. Cette "égalité" est utilisée et vérifiée expérimentalement dans des formules/expériences de physiques, ça n'est pas un raisonnement biaisé.

Je n'ai clairement pas/plus le niveau en maths pour saisir toutes les subtilités mais voilà une nuance dans la conclusion de l'article que j'ai cité plus haut :

En fait la somme 1 + 2 + 3 + 4 + … est bien infinie, mais -1/12 est ce qui la sépare de ∫ x dx qui est aussi infini, est que l’on peut voir comme une base que l’on soustrait.
[...]
Autre manière de le dire, on trouve que 1 + 2 + 3 + 4 + … est infini, mais égal à -1/12, modulo ∫ x dx.

L'utilisation du modulo pour illustrer me parle un peu plus.
C'est comme si on disait q'un nombre pair est égal à 0 modulo 2, c'est pas une égalité, plus une propriété

[Ixy]

Apparemment c'est la limite de certaines fonctions complexes en -1, en particulier de la fonction eta.

Un exemple plus simple :

A = 1 - 1 + 1 - 1 + 1 + .....

A est divergente au sens usuelle, mais on peut lui donner une valeur de plusieurs façons.

Une des façons est de faire la moyenne des limites possibles : 1 et 0 ce qui fait 0.5 (convergence au sens de Césaro). à noter que 1 + 2 + 3 + 4.... n'est pas convergent au sens de Césaro.

On peut dire aussi que c'est la limite de la fonction x^2 + x^3 + x^4 ....... = x^2(1/(1-x)) quand x tend vers -1, ce qui donne aussi 1/2.

Pour la suite 1 + 2 + 3 +4 + .... c'est pareil pour la fonction 1^(-x) + 2^(-x) + 3^(-x) + ...... mais c'est encore plus compliqué car cette fonction n'est même pas définie a priori pour tout nombre négatif, il faut faire avant cela un prolongement analytique.

[Alone3545]

j'ai l'impression que la suite dont je parlais à plusieurs solutions variable en fonction du temps sauf que le temps en faite c'est semi-subjectif. Oui deux choses se passe en mem temps on le prouve mais l'ecar entre deux faits c'est plus flou surtout si on ne compare pas entre deux écarts de temps. 2s peuvent devenir 56s par exemple.

Jai l'impresion de voir la solution de l'equation comme plusieurs résultats venant d'un nombre presque infini de courbe sinusoïdal augementant en amplification quand X le nombre de nombre à la suite devient important sachant que X est le nombre correspondant aux nombre de nombre composant la suite à l'instant t prélevé.

[Bubu]

Salut les matheuses et les matheux !
J'ai un petit problème pour vous (et moi) (mais ce n'est pas très ludique )

Comment déterminer l'intersection (sous forme de coordonnées barycentriques) d'une demi-droite et d'un triangle dans l'espace ?


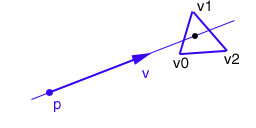
Allez ......

[Ixy]

J'ai appelé le triangle ABC.

L'intersection est le barycentre de A, B, C de poids alpha, beta gamma avec


Je te laisse trouver les autres par permutation circulaire, par exemple pour beta, A devient B, B devient C, C devient A.

[Bubu]

Merci Ixy pour ta réponse.

Je vois ça autrement je crois :

Soit O l'origine.

Pour la demi-droite :
Passant par P et de vecteur directeur d. (souligné pour vecteur)
L'intersection I s'exprime : OI = OP + a.d, a >= 0 .

Pour le triangle :
(T1, T2, T3)

L'intersection I s'exprime : OI = OT1 + u.T1T2 + v.T1T3, 0 <= u <= 1 et 0 <= v <= 1 et u + v <= 1.


Donc il faut résoudre l'équation : OP + a.d = OT1 + u.T1T2 + v.T1T3 et vérifier les conditions. (u et v sont les coordonées barycentriques).

Cela revient à résoudre ce système d'équations linéaires à 3 inconnues (a, u, et v) :

a * d.x + u * (t1.x - t2.x) + v * (t1.x - t3.x) = t1.x - p.x
a * d.y + u * (t1.y - t2.y) + v * (t1.y - t3.y) = t1.y - p.y
a * d.z + u * (t1.z - t2.z) + v * (t1.z - t3.z) = t1.z - p.z

(enfin si j'ai pas fait d’erreur(s) de calcul. )

Il y a intersection si :
Le système a bien 3 solutions (réelles).
a >= 0, u >= 0, v >= 0 et u + v <= 1.
L'intersection I a alors pour coordonnées barycentriques (u, v).